




Next: Die Fib-Operatoren
Up: Polynom Approximation
Previous: Polynom Approximation
Contents
Index
In Fib gibt es die Problemstellung, dass ein Polynom (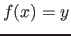 ) interpoliert werden soll, das eine feste Zahl für die Eingabe
) interpoliert werden soll, das eine feste Zahl für die Eingabe 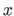 hat, aber deren Ausgabewerte
hat, aber deren Ausgabewerte 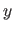 in einem Bereich liegen können. Beispielsweise ist bei Funktionen auf Ganzzahlen die Eingabe eine Ganzzahl und die Ausgabe wird auf eine Ganzzahl
in einem Bereich liegen können. Beispielsweise ist bei Funktionen auf Ganzzahlen die Eingabe eine Ganzzahl und die Ausgabe wird auf eine Ganzzahl 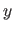 gerundet, wenn sie im Bereich
gerundet, wenn sie im Bereich
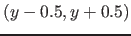 liegt. Dies kommt in Fib unter anderen vor, wenn die Helligkeit eines Punktes in Abhängigkeit von seiner Position berechnet werden soll ( z. B. mit "
liegt. Dies kommt in Fib unter anderen vor, wenn die Helligkeit eines Punktes in Abhängigkeit von seiner Position berechnet werden soll ( z. B. mit "
![$x, [1, 20],$](img851.png)
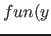
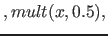
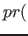
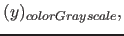
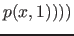 " ). Wird in diesen Fällen nicht der Freiheitsgrad für die Ausgabe ausgenutzt, sondern nur ein fester Wert aus dem möglichen Ausgabewert zur Polynominterpolation gewählt (so dass ein übliches Verfahren angewendet werden kann), kann es zu starken Schwingungen des Polynoms kommen. Dann hat das Polynom viele unnötige Faktoren, die den Speicherplatzverbrach für ein Fib-Object nur unnötig erhöhen.
" ). Wird in diesen Fällen nicht der Freiheitsgrad für die Ausgabe ausgenutzt, sondern nur ein fester Wert aus dem möglichen Ausgabewert zur Polynominterpolation gewählt (so dass ein übliches Verfahren angewendet werden kann), kann es zu starken Schwingungen des Polynoms kommen. Dann hat das Polynom viele unnötige Faktoren, die den Speicherplatzverbrach für ein Fib-Object nur unnötig erhöhen.
Deshalb wird im Nachfolgenden ein Verfahren vorgestellt, dass dies Freiheitsgraden berücksichtigt.
gegeben:
- Punkte (mit den Bereichen für den Ausgabewert):
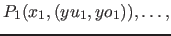
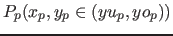
- der maximale Grad des Polynoms
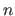 , mit
, mit 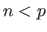
Gesucht wird das Polynom
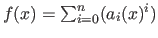 ; bzw. dessen Faktoren:
; bzw. dessen Faktoren: 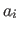 mit
mit
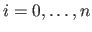 .
.
Lösung:
setze untere Grenze 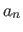 auf
auf 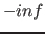 und die obere auf
und die obere auf 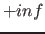
1. Lösungschema aufbauen:
2. in Dreiecksform bringen:
(  : Vergleich wird entsprechend gedreht wenn durch negative
: Vergleich wird entsprechend gedreht wenn durch negative 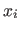 geteilt wird)
geteilt wird)
- mit
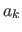 ist das
ist das 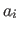 mit groessten
mit groessten 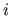 , dessen untere und ober Grenze nicht gleich ist
, dessen untere und ober Grenze nicht gleich ist
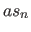 ist der konstante Faktor, der sich aus den
ist der konstante Faktor, der sich aus den 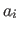 mit jeweils gleicher untere und ober Grenze und dem
mit jeweils gleicher untere und ober Grenze und dem 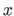 Wert der Ungleichung ergibt
Wert der Ungleichung ergibt
2.b So Umformen, dass in jeder Ungleichung ein 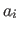 (
(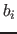 Faktor fuer die
Faktor fuer die 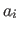 )
)
3. Lösungsschema umformen (zu  )
)
4. Faktoren Eingrenzen:
- Fuer jede Ungleichung mit maximal einen Faktor mit einer Grenze im Unendlichen:
- Passe Faktoren an; für jeden Faktor
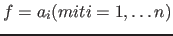 und y*; (enthaelt die Ungleichung einen inf Faktor kann nur dieser gewaehlt werden):
und y*; (enthaelt die Ungleichung einen inf Faktor kann nur dieser gewaehlt werden):
- setze anderen nicht
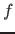 Faktoren so (auf jeweils ihre Ober- oder Untergrenze), dass sie Formel maximieren; bestimme dann
Faktoren so (auf jeweils ihre Ober- oder Untergrenze), dass sie Formel maximieren; bestimme dann 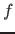 neu
neu
- wenn sich in 4. Aenderungen ergeben haben zurück zu 4.
- beginne dann mit diesem Wert Schritt 1. "Lösungschema aufbauen" erneut solange für ein
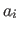 sich zuletzt Aenderungen ergeben haben oder es noch nicht eingegrenzt wurde
sich zuletzt Aenderungen ergeben haben oder es noch nicht eingegrenzt wurde
- Wenn alle
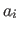 mit Grenzen belegt und keine Änderungen, wähle jeweils einen Wert (den Mittelwert) fuer
mit Grenzen belegt und keine Änderungen, wähle jeweils einen Wert (den Mittelwert) fuer 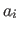 aus seinen Bereich aus; beginne mit
aus seinen Bereich aus; beginne mit 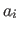 mit kleinsten
mit kleinsten 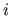 dessen Grenzen noch nicht gleich sind und gehe dann jeweils wieder zum Schritt 4
dessen Grenzen noch nicht gleich sind und gehe dann jeweils wieder zum Schritt 4





Next: Die Fib-Operatoren
Up: Polynom Approximation
Previous: Polynom Approximation
Contents
Index
Betti Österholz
2013-02-13
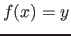 ) interpoliert werden soll, das eine feste Zahl für die Eingabe
) interpoliert werden soll, das eine feste Zahl für die Eingabe 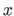 hat, aber deren Ausgabewerte
hat, aber deren Ausgabewerte 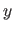 in einem Bereich liegen können. Beispielsweise ist bei Funktionen auf Ganzzahlen die Eingabe eine Ganzzahl und die Ausgabe wird auf eine Ganzzahl
in einem Bereich liegen können. Beispielsweise ist bei Funktionen auf Ganzzahlen die Eingabe eine Ganzzahl und die Ausgabe wird auf eine Ganzzahl 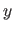 gerundet, wenn sie im Bereich
gerundet, wenn sie im Bereich
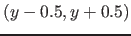 liegt. Dies kommt in Fib unter anderen vor, wenn die Helligkeit eines Punktes in Abhängigkeit von seiner Position berechnet werden soll ( z. B. mit "
liegt. Dies kommt in Fib unter anderen vor, wenn die Helligkeit eines Punktes in Abhängigkeit von seiner Position berechnet werden soll ( z. B. mit "
![$x, [1, 20],$](img851.png)
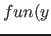
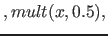
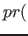
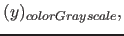
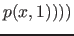 " ). Wird in diesen Fällen nicht der Freiheitsgrad für die Ausgabe ausgenutzt, sondern nur ein fester Wert aus dem möglichen Ausgabewert zur Polynominterpolation gewählt (so dass ein übliches Verfahren angewendet werden kann), kann es zu starken Schwingungen des Polynoms kommen. Dann hat das Polynom viele unnötige Faktoren, die den Speicherplatzverbrach für ein Fib-Object nur unnötig erhöhen.
" ). Wird in diesen Fällen nicht der Freiheitsgrad für die Ausgabe ausgenutzt, sondern nur ein fester Wert aus dem möglichen Ausgabewert zur Polynominterpolation gewählt (so dass ein übliches Verfahren angewendet werden kann), kann es zu starken Schwingungen des Polynoms kommen. Dann hat das Polynom viele unnötige Faktoren, die den Speicherplatzverbrach für ein Fib-Object nur unnötig erhöhen.





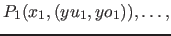
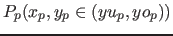
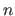 , mit
, mit 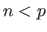
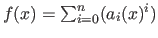 ; bzw. dessen Faktoren:
; bzw. dessen Faktoren: 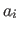 mit
mit
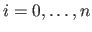 .
.
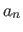 auf
auf 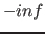 und die obere auf
und die obere auf 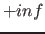
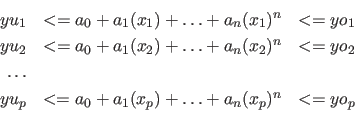
 : Vergleich wird entsprechend gedreht wenn durch negative
: Vergleich wird entsprechend gedreht wenn durch negative 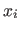 geteilt wird)
geteilt wird)
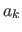 ist das
ist das 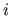 , dessen untere und ober Grenze nicht gleich ist
, dessen untere und ober Grenze nicht gleich ist
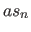 ist der konstante Faktor, der sich aus den
ist der konstante Faktor, der sich aus den 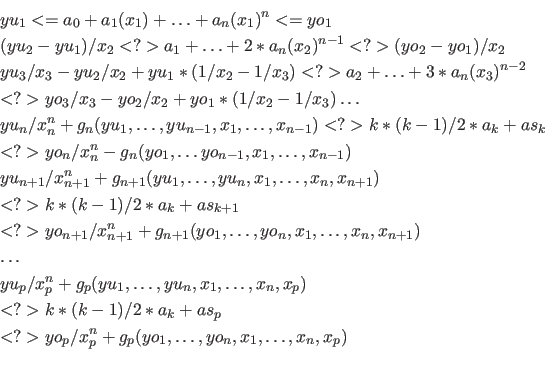
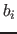 Faktor fuer die
Faktor fuer die 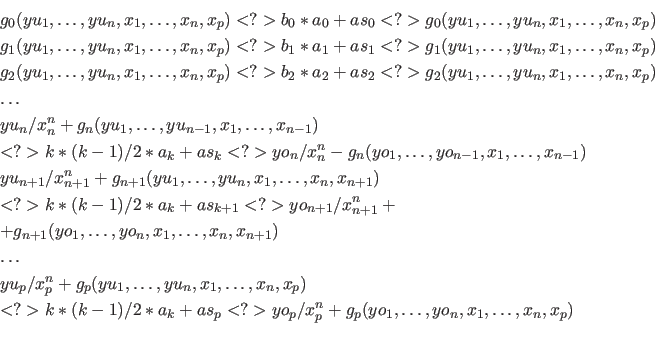
 )
)
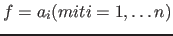 und y*; (enthaelt die Ungleichung einen inf Faktor kann nur dieser gewaehlt werden):
und y*; (enthaelt die Ungleichung einen inf Faktor kann nur dieser gewaehlt werden):
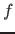 Faktoren so (auf jeweils ihre Ober- oder Untergrenze), dass sie Formel maximieren; bestimme dann
Faktoren so (auf jeweils ihre Ober- oder Untergrenze), dass sie Formel maximieren; bestimme dann